Ein Würfel aus Glas mit einem Brechungsindex von n2 = 1,5 und einer Kantenlänge von a = 6 cm hat in seiner Mitte eine kleine Fliege eingeschlossen (der Würfel befindet sich in Luft mit n1 = 1). Angenommen sei, dass es sich um ein punktförmiges Gebilde handelt. Nachfolgend soll die Frage betrachtet werden, welche Teile einer Würfelfläche bedeckt werden müssen, damit die Fliege von keiner Richtung aus mehr gesehen werden kann.
Zunächste sei ein Koordinatensystem (x,y,z) derart gewählt, daß der Koordinatenursprung im Mittelpunkt des Würfels liegt und die Achsen senkrecht auf den Würfelflächen stehen. Betrachtet sei das Problem als 2D-Schnitt durch die Mitte des Würfels. Da es sich um ein vollständig symmetrisches Problem handelt, kann o.B.d.A. das Problem auf einen 2D-Schnitt reduziert werden und hieraus das Ergebnis abgeleitet werden.

Es gilt nach dem Brechungsgesetz
![]()
und aus der Geometrie des Problems (siehe Abb.)
![]()
Einsetzen der zweiten Gleichung in die erste und Umstellung nach z liefert
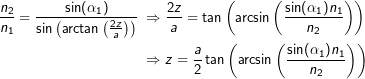
Da die Fliege nicht mehr gesehen werden soll, muß ![]() gehen, damit alle Lichtstrahlen erfaßt werden:
gehen, damit alle Lichtstrahlen erfaßt werden:
![]()
Geprüft werden muß noch, ob beim Übergang Glas-Luft nun Totalreflexion auftritt, da ![]() sonst nicht so groß gewählt werden kann.
sonst nicht so groß gewählt werden kann.

D. h. bei ![]() tritt Totalreflextion auf und somit muß
tritt Totalreflextion auf und somit muß ![]() gelten. Da oben jedoch ein Grenzprozeß vorgenommen wurde und z = zG ist, ist der berechnete z-Wert der Grenzwert, wo die Fliege gerade nicht mehr gesehen werden kann.
gelten. Da oben jedoch ein Grenzprozeß vorgenommen wurde und z = zG ist, ist der berechnete z-Wert der Grenzwert, wo die Fliege gerade nicht mehr gesehen werden kann.
Da es sich um ein rotationssymmetrisches Objekt handelt (bei Rotation um x,y,z-Achse), sind die abzudeckenden Flächen Kreise mit Radius ![]() und Mittelpunkt in den Objektachsen. Es ist ausreichen, auf drei orthogonal zueinander stehenden Würfelflächen diese mit den Kreisscheiben abzudecken.
und Mittelpunkt in den Objektachsen. Es ist ausreichen, auf drei orthogonal zueinander stehenden Würfelflächen diese mit den Kreisscheiben abzudecken.


